Cervelli Matematici: il Fascino Insondabile della Matematica e il Cervello Umano

La matematica è stata a lungo considerata il linguaggio universale della scienza. Ma quanto è innata questa capacità nel cervello umano? Gli studi condotti da università come il MIT e la Stanford University suggeriscono che la predisposizione alla matematica potrebbe essere più profondamente radicata nel nostro DNA di quanto pensassimo. Questo articolo esplora la complessa relazione tra la matematica e la neurobiologia, con un occhio di riguardo alle implicazioni geografiche, sociologiche, e naturalistiche.

La Neurobiologia della Matematica: Un Viaggio nel Cervello

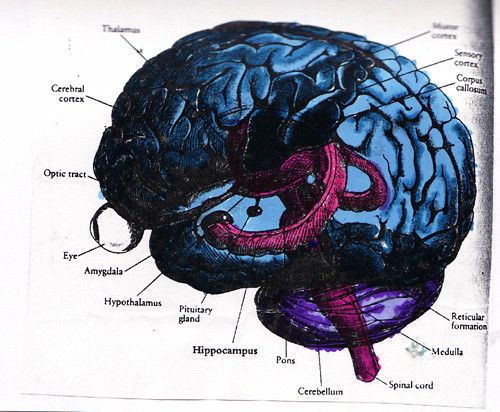
Il cervello umano è un organo di straordinaria complessità, una macchina biologica che continua a sfidare la nostra comprensione completa. Tra le sue molteplici funzioni, alcune aree cerebrali come il lobo parietale e la corteccia prefrontale dorsolaterale sono strettamente coinvolte nel ragionamento matematico. Questo non è un dettaglio minore; è una scoperta che potrebbe gettare luce su come siamo cablati per comprendere l’universo.

Uno studio pubblicato sulla rivista “Nature Neuroscience” ha esplorato le specifiche strutture neurali che sono attive durante la soluzione di problemi matematici. Questa ricerca ha rivelato che la nostra capacità di affrontare questioni matematiche non è solo il risultato dell’educazione o dell’ambiente, ma potrebbe essere legata a specifiche reti neurali. Il neuroscienziato Stanislas Dehaene ha contribuito significativamente a questo campo, suggerendo che il cervello umano possiede un “senso del numero” innato.

Ma da dove proviene questa predisposizione? La risposta potrebbe risiedere nei nostri geni. Studi di gemelli condotti dalla Washington University hanno mostrato che la capacità matematica ha una forte componente genetica. Questi studi, guidati dal Dr. Stephen Malone, hanno utilizzato tecniche di imaging cerebrale per esaminare le somiglianze e le differenze nella struttura cerebrale dei gemelli, fornendo una prova convincente del ruolo dei fattori genetici nel ragionamento matematico.

Non solo la genetica, ma anche l’epigenetica, il modo in cui i geni sono espressi a causa di fattori ambientali, potrebbe avere un ruolo. Un paper pubblicato nel “Journal of Cognitive Neuroscience” ha esplorato come l’ambiente precoce, incluso lo stress materno durante la gravidanza, potrebbe influenzare la formazione delle reti neurali associate alla matematica.

Infine, è fondamentale considerare l’interazione tra queste strutture neurali e il sistema educativo. La pedagogia matematica può essere ottimizzata per sfruttare queste reti neurali innate? Questa è una domanda che la ricerca futura dovrà affrontare, ma alcuni studi preliminari suggeriscono che un approccio educativo personalizzato potrebbe essere più efficace nel nutrire queste abilità innate.

In sintesi, il cervello umano è un ecosistema complesso di reti neurali, fattori genetici ed epigenetici, tutti interconnessi in un delicato equilibrio che contribuisce alla nostra comprensione della matematica. Questo non è solo un campo di ricerca accademica, ma una frontiera che potrebbe rivoluzionare il modo in cui insegniamo e apprendiamo questa disciplina fondamentale.

L’Influenza Geografica e Socioculturale

La geografia e la cultura sono elementi che spesso vengono trascurati quando si parla di competenze in matematica, ma la loro importanza è innegabile. Prendiamo ad esempio la Finlandia e Singapore, due nazioni che si distinguono per l’eccellenza nell’educazione scientifica. Queste nazioni non solo investono pesantemente in risorse educative, ma hanno anche una cultura che pone un grande valore sulla scienza e la tecnologia.

Uno studio condotto dall’Università di Oxford ha esaminato l’incidenza di fattori geografici e culturali sulle competenze matematiche. La ricerca ha evidenziato come l’accesso a materiali educativi di alta qualità e docenti qualificati possa fare una differenza significativa. Inoltre, la presenza di musei scientifici, laboratori e biblioteche specializzate può stimolare l’interesse per la matematica già da una giovane età.

Ma non è solo una questione di risorse. La cultura gioca un ruolo fondamentale. In un paper pubblicato nel “Journal of Educational Psychology”, i ricercatori hanno esplorato come l’atteggiamento culturale verso la matematica possa influenzare le prestazioni accademiche. In paesi come Singapore, l’importanza della matematica è radicata nella filosofia educativa e viene vista come una competenza essenziale per il successo personale e professionale.

Un altro aspetto interessante è l’integrazione della matematica con altre discipline. In Finlandia, ad esempio, l’educazione scientifica è spesso integrata con l’apprendimento pratico e l’educazione ambientale. Questo approccio olistico non solo migliora la comprensione della matematica, ma la rende anche più applicabile e rilevante nella vita quotidiana.

Infine, vale la pena notare che anche il clima politico può avere un impatto. Paesi con un forte sostegno governativo all’innovazione scientifica e alla ricerca tendono ad avere popolazioni più competenti in matematica. Questo è stato confermato da uno studio del MIT, che ha esaminato come le politiche pubbliche possano influenzare l’educazione scientifica.

In sintesi, la geografia e la cultura non sono fattori periferici, ma elementi centrali che contribuiscono alla formazione di competenze matematiche. Dall’accesso a risorse educative di alta qualità all’importanza culturale attribuita alla matematica, questi fattori creano un ecosistema che può sia nutrire che ostacolare lo sviluppo matematico.

Matematica e Natura: Un Legame Inaspettato

La matematica è spesso vista come un prodotto esclusivo dell’intelligenza umana, ma un’osservazione più attenta del mondo naturale rivela una realtà sorprendente. La flora e la fauna esibiscono schemi matematici che vanno ben oltre la semplice simmetria. Uno degli esempi più noti è la sequenza di Fibonacci, una serie di numeri in cui ogni numero è la somma dei due precedenti. Questa sequenza è visibile in molti aspetti della natura, dai petali dei fiori alle conchiglie marine.

Il matematico e filosofo Benoit Mandelbrot è stato uno dei primi a esplorare questa connessione in modo sistematico. Nel suo libro “The Fractal Geometry of Nature”, Mandelbrot ha esaminato come i frattali, strutture geometriche complesse, siano presenti in fenomeni naturali come le coste marine e le strutture delle piante. Questi frattali seguono leggi matematiche precise, suggerendo che la matematica è intrinsecamente legata alla struttura del mondo naturale.

Un altro esempio affascinante è il numero aureo, o Phi, che è circa 1,618. Questo numero è stato osservato in varie strutture biologiche, dalla disposizione delle foglie sugli alberi alla forma delle galassie. Il biologo Adrian Bejan ha teorizzato nel suo paper “The Golden Ratio Predicts Prolificacy in Feral Animals” che il numero aureo può anche essere correlato alla riproduzione negli animali.

La simmetria è un altro concetto matematico che trova applicazione in natura. Ad esempio, la simmetria radiale è comune nei fiori e negli animali marini come le stelle marine.

Questa simmetria non è solo esteticamente gradevole, ma ha anche funzioni biologiche. Uno studio pubblicato nel “Journal of Theoretical Biology” ha esplorato come la simmetria possa essere vantaggiosa per la sopravvivenza di alcune specie.

Ma non è solo la biologia a essere influenzata dalla matematica. Anche i fenomeni atmosferici come i turbini e i vortici seguono leggi matematiche.

Turbini e Vortici: La Matematica Nascosta dei Fenomeni Atmosferici

I fenomeni atmosferici come turbini e vortici sono spesso considerati eventi caotici e imprevedibili. Tuttavia, una più attenta analisi rivela che questi fenomeni seguono leggi matematiche precise, offrendo una visione affascinante della complessità intrinseca della natura. Questo non è solo un dettaglio per gli appassionati di scienza; è una chiave per comprendere e prevedere eventi atmosferici che possono avere un impatto significativo sulla vita umana.

Uno dei pionieri in questo campo è stato il matematico e meteorologo Edward Lorenz, che ha sviluppato la Teoria del Caos. Nel suo paper seminale del 1963, “Deterministic Nonperiodic Flow”, Lorenz ha dimostrato che sistemi apparentemente semplici possono produrre comportamenti estremamente complessi e imprevedibili. Questa scoperta ha avuto un impatto profondo sulla meteorologia, suggerendo che la previsione del tempo potrebbe essere intrinsecamente limitata dalla natura caotica dei sistemi atmosferici.

Un altro contributo significativo è stato fatto da Vladimir Arnold, che ha sviluppato la teoria dei vortici di KAM (Kolmogorov-Arnold-Moser). Questa teoria ha fornito un quadro matematico per comprendere la stabilità e la struttura dei vortici in fluidi come l’aria e l’acqua. Il suo lavoro ha trovato applicazioni non solo in meteorologia ma anche in oceanografia e astrofisica.

Recentemente, la dinamica dei fluidi computazionale (CFD) è diventata uno strumento fondamentale per studiare questi fenomeni. Un paper pubblicato da George Haller nel “Journal of Fluid Mechanics” ha utilizzato tecniche di CFD per modellare la formazione e l’evoluzione di turbini e vortici, offrendo nuove intuizioni su come questi fenomeni possano essere influenzati da variabili come la temperatura e la pressione atmosferica.

In sintesi, i turbini e i vortici, lontani dall’essere semplici anomalie atmosferiche, sono manifestazioni di leggi matematiche profonde che governano il comportamento dei fluidi. Da Lorenz a Arnold, da teorie caotiche a modelli computazionali, la matematica continua a svelare i segreti nascosti dietro questi affascinanti fenomeni atmosferici.

La presenza di schemi matematici nella natura ci costringe a riconsiderare il nostro ruolo nell’universo e la portata della matematica stessa. Non è solo un utensile creato dall’uomo per descrivere il mondo, ma un elemento fondamentale dell’essenza del mondo in cui viviamo. Da Fibonacci a frattali, da Phi alla simmetria, la matematica è un linguaggio universale che la natura sembra parlare in modo eloquente.

Implicazioni Politiche e Militari

La matematica non è solo il fondamento di scienze come la fisica o l’ingegneria; è anche una componente cruciale nelle decisioni politiche e militari. L’analisi dei dati, ad esempio, è diventata una parte integrante della strategia militare moderna. Algoritmi sofisticati sono utilizzati per il posizionamento ottimale delle truppe, la pianificazione di missioni e l’analisi di risorse naturali. Questi algoritmi sono spesso basati su principi matematici avanzati come la teoria dei giochi, la teoria delle reti e la statistica bayesiana.

La Naval Postgraduate School (NPS) negli Stati Uniti è una delle istituzioni leader nella ricerca avanzata in questo campo. Uno dei progetti più noti dell’NPS è l’applicazione della teoria dei giochi alla strategia militare. Questa teoria, inizialmente sviluppata da John von Neumann e Oskar Morgenstern, è utilizzata per simulare vari scenari di conflitto e negoziazione. Il lavoro di Bruce Bueno de Mesquita, un politologo e professore alla New York University, ha ulteriormente esteso l’applicazione della teoria dei giochi alla politica internazionale, fornendo intuizioni su come le nazioni prendono decisioni strategiche.

Non solo le forze armate, ma anche le agenzie di intelligence fanno uso intensivo della matematica. La crittografia, ad esempio, è un campo che si basa pesantemente su concetti matematici per garantire la sicurezza delle comunicazioni. Clifford Cocks, un matematico britannico, ha sviluppato uno dei primi algoritmi di crittografia a chiave pubblica, che è diventato fondamentale per la sicurezza informatica a livello globale.

Inoltre, la matematica gioca un ruolo nella gestione delle risorse naturali, un tema di crescente importanza geopolitica. L’analisi matematica è utilizzata per ottimizzare l’estrazione di risorse come petrolio e gas naturale. Questo è particolarmente rilevante in contesti politicamente sensibili come il Mar Cinese Meridionale, dove la presenza di risorse naturali è un fattore chiave nelle tensioni regionali.

Infine, è importante notare che la matematica è anche utilizzata per modellare e prevedere comportamenti sociali durante periodi di conflitto. Uno studio pubblicato nel “Journal of Artificial Societies and Social Simulation” ha utilizzato modelli matematici per analizzare le dinamiche delle proteste e delle rivolte, fornendo dati preziosi che possono influenzare le decisioni politiche.

In sintesi, la matematica è diventata un elemento insostituibile nella strategia e nella presa di decisioni in ambiti politici e militari. Dalla teoria dei giochi alla crittografia, dalla gestione delle risorse naturali alla modellazione del comportamento sociale, la sua applicazione è vasta e in continua evoluzione.

Teoria dei Giochi: Un Ponte tra Matematica, Neurobiologia e Genetica

La Teoria dei Giochi, un campo matematico che studia le decisioni strategiche, ha trovato applicazioni in una varietà di discipline, dalla economia alla biologia evolutiva. Ma una delle aree più intriganti è la sua connessione con la neurobiologia e la predisposizione genetica. Questo non è un semplice esercizio accademico; è una finestra aperta sul modo in cui il cervello umano è cablato per prendere decisioni.

Uno studio pionieristico pubblicato nel “Journal of Neuroscience” da Colin Camerer, un economista comportamentale, ha esplorato come il cervello umano elabora le decisioni strategiche. Utilizzando la risonanza magnetica funzionale (fMRI), la ricerca ha identificato l’attivazione di specifiche aree cerebrali, come la corteccia prefrontale ventromediale, durante giochi di strategia. Questo suggerisce che esistono circuiti neurali dedicati al ragionamento strategico, una scoperta che potrebbe avere implicazioni per l’educazione e la formazione professionale.

Ma da dove proviene questa capacità? Alcuni indizi possono essere trovati nella genetica. Un paper pubblicato da Sarah Mathew e Robert Boyd nel “Proceedings of the National Academy of Sciences” ha esaminato come la predisposizione genetica possa influenzare il comportamento strategico. Utilizzando dati da studi su gemelli, i ricercatori hanno scoperto che esiste una correlazione significativa tra specifici marcatori genetici e la propensione a comportamenti cooperativi o competitivi.

Non meno interessante è l’intersezione tra la Teoria dei Giochi e l’intelligenza artificiale. La ricerca condotta da Yoshua Bengio, un pioniere nel campo del deep learning, suggerisce che gli algoritmi di apprendimento automatico possono essere ottimizzati utilizzando principi derivati dalla Teoria dei Giochi, aprendo la strada a nuove frontiere nella robotica e nella decisione automatizzata.

La Teoria dei Giochi non è solo un campo matematico astratto; è un prisma attraverso il quale possiamo esaminare la complessità del cervello umano e la natura stessa della decisione. Dalla neurobiologia alla genetica, questo campo offre spunti di riflessione che potrebbero rivoluzionare la nostra comprensione di come prendiamo decisioni, sia come individui che come società.

Teoria dei Giochi e Intelligenza Artificiale: Un’Alleanza per la Decisione Avanzata

La Teoria dei Giochi, tradizionalmente un dominio della matematica applicata e dell’economia, sta diventando un pilastro fondamentale nell’evoluzione dell’Intelligenza Artificiale (IA) e della decisione automatizzata. Questa convergenza non è casuale; rappresenta un’intersezione cruciale tra il ragionamento umano e la capacità delle macchine di prendere decisioni complesse.

Un paper influente di Michael Bowling, pubblicato nel “Journal of Artificial Intelligence Research”, ha esplorato come gli algoritmi di apprendimento possano essere addestrati utilizzando principi della Teoria dei Giochi. Questo lavoro ha gettato le basi per lo sviluppo di sistemi di IA che possono negoziare, competere e cooperare con gli esseri umani o altre IA in scenari complessi.

Ma la Teoria dei Giochi non è solo un mezzo per migliorare l’apprendimento automatico; è anche un modo per comprendere i limiti etici e le implicazioni della decisione automatizzata. Un progetto di ricerca condotto da Dylan Hadfield-Menell presso il MIT ha utilizzato la Teoria dei Giochi per studiare i dilemmi etici nell’uso di IA, come la distribuzione equa delle risorse o le decisioni in scenari di vita o di morte.

Un altro sviluppo entusiasmante è l’uso della Teoria dei Giochi nella robotica. Vijay Kumar, un ingegnere presso l’Università della Pennsylvania, ha applicato principi della Teoria dei Giochi per coordinare i movimenti di squadre di droni. Questo ha implicazioni non solo per applicazioni civili come la consegna di pacchi, ma anche per usi militari e di soccorso in caso di disastri.

Infine, la Teoria dei Giochi sta trovando applicazioni anche in reti neurali generative, un sotto-campo dell’IA che si occupa della creazione di nuovi dati che assomigliano a un set di dati di addestramento. Ian Goodfellow, uno dei pionieri in questo campo, ha utilizzato la Teoria dei Giochi per sviluppare il concetto di Generative Adversarial Networks (GANs), che ha rivoluzionato la generazione di immagini e suoni artificiali.

La Teoria dei Giochi e l’Intelligenza Artificiale stanno formando una simbiosi che potrebbe ridefinire il modo in cui le decisioni sono prese, sia da macchine che da esseri umani. Da algoritmi di apprendimento a questioni etiche, da applicazioni robotiche a generazione di dati, questa alleanza promette di spingere i confini di ciò che è possibile in un mondo sempre più automatizzato.

Un Universo da Esplorare

La predisposizione del cervello umano alla matematica è un campo di ricerca in rapida evoluzione. Con implicazioni che vanno dalla neurobiologia alla geopolitica, è un argomento che merita una considerazione seria e approfondita. Come dimostrano gli studi, la matematica è più di un semplice strumento: è una parte fondamentale della nostra essenza. In sintesi, mentre ci possono essere differenze cerebrali che si correlano con le abilità matematiche, non è possibile ridurre la questione a una semplice questione di “predisposizione” o “non predisposizione”. La questione è multidimensionale e richiede una comprensione olistica di fattori genetici, neurologici, psicologici, educativi, sociali e culturali.

🌿 Natura: Immergiti nei segreti del nostro pianeta.
🔬 Tecnologia: Esplora le innovazioni che stanno plasmando il nostro futuro.
🗺️ Geografia: Viaggia con noi attraverso paesaggi mozzafiato e culture affascinanti.
🎭 Cultura: Immergiti nella ricchezza della diversità umana.
📜 Storia: Scopri storie avvincenti che hanno plasmato il mondo che conosciamo.
🌟 Speciali: Approfondimenti, dossier e reportage esclusivi su temi di grande attualità.

In un mondo pieno di informazioni confuse e spesso sbagliate, Deductio lavora per spiegare la scienza in modo semplice e preciso. Crediamo che tutti abbiano il diritto di capire come funziona il mondo che li circonda. Non è sempre facile, ma è quello che cerchiamo di fare ogni giorno. Se pensi che valga la pena sostenerci, aiutaci a continuare.